Blender:Geometry Node 應用於營造法式生成大木作構件初探-梭柱篇
摘要
本文初步探索了透過使用 Blender 內建 Geometry Node 來程序化生成建築構件。
前言
最近正在學習 Blender 的 Geometry Node,使用程序化生成模型非常的吸引我,看了一些教學後在想時不是要做些什麼當作練習。第一個想到的其實是應用在建築構件的生成。
營造法式的大木作構件感覺就是一個很好的題材,因為大木作構建本身在營造法式中已經很詳細載明了做法。所以很適合做成程序化生成模型,此外我想到另一個優點是可以快速透過調整參數控制品質,例如曲線的段數和榫卯可以透過參數調整,便於處理 LOD 或是不同使用情境。
這次初探會針對梭柱嘗試製作程序化生成模型,首先我們要了解營造法式中針對梭柱的規則,再來藉由這些規格轉化成程程序化生成模型的邏輯。
該專案也有上傳至 Github
術語簡單介紹
因為再來會很常使用到中國傳統建築的一些術語,所以先在此簡單解釋:
- 卷殺:是指對構件砍削出折線或曲線的行為,藉以柔化外觀
- 材分:宋代《營造法式》中使用的這個建築尺度單位,主要用來控制建築構件尺寸的模數。1 材可細分為 15 分,但是這個一材的大小隨著等級可大可小。另外還有栔,為 10 分。
梭柱的規格
梭柱的規定在 《營造法式》第五卷·大木作制度二 有敘述,這邊只擷取與梭柱相關,亦不擷取與升起側腳相關的部分。
凡用柱之製,若殿閣即徑兩材兩栔至三材,若廳堂柱即徑兩材一栔,餘屋即徑一材一栔至兩材。若廳堂等屋內柱,皆隨舉勢定其短長,以下檐柱為則。(若副階廊舍,下檐柱雖長,不越間之廣。……
凡殺梭柱之法,隨柱之長,分為三分。上一分又分為三分,如栱卷殺,漸收至上,徑比櫨枓底四周各出四分;又量柱頭四分,緊殺如覆盆樣,令柱頭與櫨枓底相副。其柱身下一分殺令徑圍與中一分同。 ……
從以上敘述可以知道柱子有三個主要的參數,直徑與高(長)、材分等級來決定一分(U)的大小,然而高卻沒有非常詳細的規定,此處以實例常見的直徑(D)與高度(H)比為 1:9 假定。
H = 9 * D
D = 42 ~ 45 * U
有關卷殺,柱身上方寫的非常清楚,柱身下方卻不是很明瞭,我們此處假設只有上方有卷殺,也就是如上敘述的柱身上方 1/3 的部分進行卷殺。
另外一個問題來了「徑比櫨枓底四周各出四分」,櫨枓尺寸在《營造法式》第四卷·大木作制度一 有敘述。
一曰櫨枓:施之於柱頭,其長與廣皆三十二分。若施於角柱之上者,方三十六分,〈(如造圜枓,則面徑三十六分,底徑二十八分。)〉高二十分。上八分為耳,中四分為平,下八分為欹。〈(今俗謂之溪者非。)〉開口廣十分,深八分,〈(出跳則十字開口,四耳。如不出跳,則順身開口,兩耳。)〉底四面各殺四分,欹䫜一分。〈(如柱頭用圜枓,即補間鋪作用訛角枓。)
可以知道平柱櫨枓底的尺寸為 24 * 24 分,角柱的櫨枓底尺寸為 28 * 28 分。加上「又量柱頭四分,緊殺如覆盆樣」,可以知道從櫨枓底寬高各有 4 分的覆盆卷殺,這個四分的高度包含在柱頭上方原本卷殺的「上一分又分為三分」裡。
初步繪製梭柱剖面
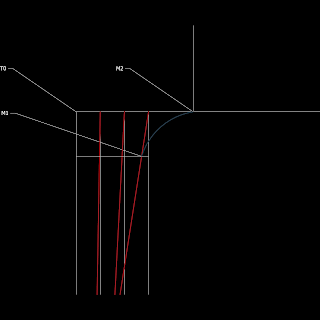
至此已經可以開始準備繪製出梭柱的單側剖面,各個點與尺寸使用代號替代。「上一分又分為三分」將柱頭等分為三分,共三個點,由下至上命名為 P0、P1、P2。對應的柱頭上皮(未卷殺時)從外到櫨枓底出四分的位置,亦須等分為三等分,才能放樣繪製折線,共四個點,由外往內命名為 T0、T1、T2、T3。
卷殺時分別繪製以下線段就能初步繪製出梭柱的放樣線(紅線)
P0T1
P1T2
P2T3
放樣線會產生兩個交點 I1、I2。藉此可以求出梭柱的三段折線,但還缺覆盆狀卷殺:
P0I1
I1I2
I2T3
覆盆的卷殺還需要兩個端點,一個為由柱頭上皮向下四分,再向內直到與折線相交的交點,一個則是櫨枓底的最外側,前者命名為 M1 後者為 M2。繪製 M1M2 即為覆盆狀卷殺的剖線(藍線)。
到此便可以得到柱頭卷殺後的剖面線,由以下四個線段組成:
P0I1
I1I2
I2M1
M1M2
程序化生成剖面線
以上都是透過手工作圖來求得卷殺的剖面線,然而如果這些剖面線段的端點座標改成用變數表達,就可以透過程序化生成剖面線。
我們可以先把已知的點的座標寫出來,以柱子下皮中心點為原點(0, 0),目前可以發現 M1、I1、I2 尚不確定:
U為 1 分的尺寸、D 為直徑(42 ~ 45 * U)、H 為高。
P0(-1/2D, 2/3H)
P1(-1/2D, 7/9H)
P2(-1/2D, 8/9H)
T0(-1/2D, H)
T1((T0.x - T3.x) * (2/3) + T3.x, H)
T2((T0.x - T3.x) * (1/3) + T3.x, H)
T3(-16U, H) (若為角柱則因為櫨枓底較大, 為 -18U)
M2(-12U, H) (若為角柱則因為櫨枓底較大, 為 -14U)
方法一、嘗試透過方程組求解
我們可以藉由將放樣的線段轉成方程組求交點進而得知這些點的座標(也有其他方式求解就是了)。
I1 為以下兩個線段的交點
P0T1:y = H((2X+D) / (D-32U) + 2/3)
P1T2:y = H((2X+D) / (3D-96U) + 7/9)
得 I1座標(-5D/12-8U/3, 5/6H)
I2 為以下兩個線段的交點
P1T2:y = H((2X+D) / (3D-96U) + 7/9)
P2T3:y = H((2X + 32U) / (9D-288U) + 1)
得 I2座標(-(D/4 + 8U), 17H /18)
M1為以下兩個線段的交點
P2T3:y = H((2X + 32U) / (9D-288U) + 1)
y=H-4U
得 M1座標(2U(288U-9D-8H) / H, H-4U)
發現求交點的解其實要透過手動計算,不怎麼輕鬆。雖然常見的四點雙線求交點有現成的公式就是了。所以也思考了 M1、I1、I2 可以透過放樣線再通過 Geometry Node 直接求出點的可能性。
方法二、使用 Geometry Node 求點
用 Geometry Node 求 M1、I1、I2 的座標,簡單來說基本也可以使用求交點的方式,不過 Blender 的 Geometry Node 並沒有可以直接透過線段求交點的 Node,一個最暴力的方法是將線段轉為 Mesh,再透過 Mesh Boolean 做 Intersection,然後再將輸出結果的 Mesh 取得 Bounding Box,取出中點就可以得到近似值,如此文章所述。
另一個方法是真的使用放樣線對柱頭剖面連續使用 Mesh Boolean 的 Subtraction,砍削的是 T0與放樣線的兩端點圍合的三角形,有點類似模仿現實的"殺"的動作。
使用 Geometry Node 繪製剖面線段
這邊因為已經計算好各點了,因此採用的是方法一。
分的 Node
初步產生折線線段
這邊看起來複雜,其實很簡單,就是要輸入兩個主要的參數高(H)和直徑(D,單位為分) ,就能依照以上算式算出各個點,並且連起來,直到目前為止線段都是直線。可以發現目前P0 到 M1有四個點,其實可以當作貝茲曲線的控制點,但我們目前先暫時繪製直線。
覆盆狀剖面線繪製
M1M2 為曲線,要如何繪製呢?其實就是繪製內切 M1、T3、M2 三點的曲線,使用 Quadratic Bézier,兩個端點為 M1 及 M2,中間的控制點使用 T3。圖片中還順便繪製柱頭上皮的線段,如此一來剖面線便完成。
線段連接
線段繪製好後需要連接,將線段轉為 Mesh 後再對頂點進行 Merge,這邊還有變換的頂點,主要是換算單位,因為 Geometry Node 的單位都是 M,但是計算時使用公分,除此之外還在 X 軸旋轉 90 度,以便後面旋轉成型。
旋轉成型
至此梭柱的程序化生成模型已經大致完成,不過還可以添加控制 LOD 的選項。
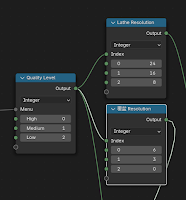
LOD
梭柱模型在面數的部分有幾點可以調整,
- 旋轉成型的段數(Resolution)
- 覆盆曲線的段數
- 覆盆曲線的有無,這意味著 M1M2 和 I2M1 會移除,取而待之為單一線段 I2T3
最後成果
完成的梭柱程序化生成模型,可以看見在 Modifier 視窗中調整 Quality 即能控制面數精細。
未來研究方向
對於折線的點座標計算應該要有高效快速的方法。另外目前其實柱子沒有製作榫卯,也就是管腳榫和柱頭固定櫨枓的饅頭榫,也沒有處理側腳和升起,因為目前只有製作單根柱子,未來處理這方面要考慮到自動計算柱子升起後的高度,並且提供側腳的參數來將柱腳偏移。
另外我後來想到,卷殺的放樣線都是長寬以 N * N 等分的方式構成,也許可以計算出公式,再將長寬代入即可。











留言
張貼留言
₍₍ς(OωO ς)⁾⁾